CEL方法研究及其在汇聚压缩问题中的应用

 共1页  1 

汇聚压缩是一个存在高温高压、大压缩比、高密度比、高压力比等极端条件的物理问题，对模拟程序提出了苛刻的要求。在爆轰加载的作用下，外层金属飞层变形较小，中心气区会发生微喷、流体力学不稳定性、混合等大变形、高度非线性的现象。拉氏方法基于变形网格，能够准确追踪界面演化，擅长描述外层金属飞层的演化；欧拉方法基于固定网格，擅长描述中心气区的高度大变形问题。采用单一方法很难同时准确给出金属飞层的演化规律和气区的精细流场结构。

CEL方法根据介质的变形特点，将介质分别采用欧拉和拉氏方法计算，在欧拉/拉氏计算域的重叠区域实现欧拉/拉氏介质的相互作用，实现充分结合欧拉、拉氏方法各自优点的目的。目前，鲜见到CEL方法在汇聚压缩领域应用的文献。本文基于Ghost Cell思想，针对汇聚压缩问题，发展了CEL方法，编写了CEL耦合程序。将该程序用于汇聚压缩问题的模拟工作，为进一步研究相关重要工程问题探索新的思路。

1  CEL方法研究

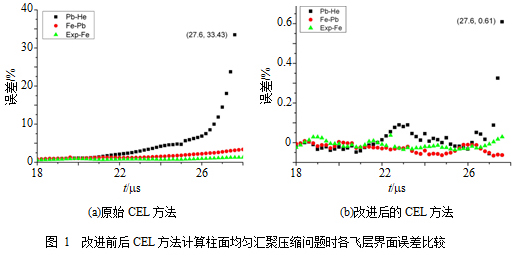
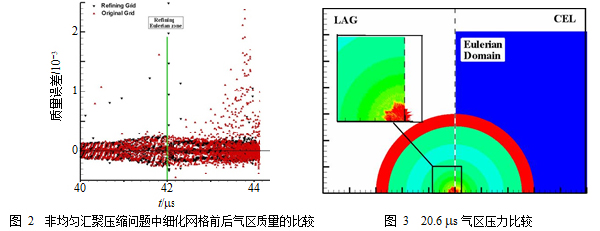
基于Ghost Cell思想的耦合方法具有抵抗大变形能力强、鲁棒性好、容易实现等优点。然而，在欧拉/拉氏接触面上往往存在显著的质量损失问题。我们采用HLLC近似黎曼解法器耦合欧拉/拉氏接触面上欧拉和拉氏流场的力学状态，得到接触面上欧拉流场对拉氏介质的作用力；其次，在Ghost流场增加速度松弛项，将质量损失控制在一个较小的范围内振荡；再次，研制欧拉网格自适应细化算法提高汇聚压缩后期欧拉气区流场的计算精度，降低欧拉流场的计算误差。大量数值实验表明：1)以上改进措施显著提高了欧拉/拉氏接触面耦合精度(如图1，均匀压缩问题中飞层界面走时误差下降约两个数量级)；2)上述措施有效抑制了欧拉流场的质量损失问题(如图2，非均匀压缩问题中气区质量误差可控制在0.5%以内)。

2  CEL方法在汇聚压缩问题中的初步应用

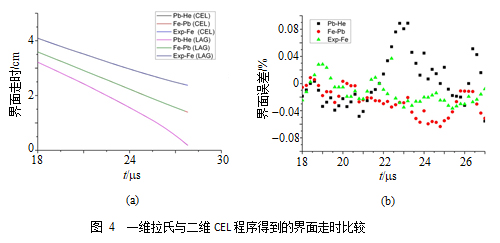
        采用CEL程序分别模拟柱面均匀和非均匀汇聚压缩两类问题。在模拟柱面均匀压缩问题时，中心欧拉气区采用36万个100 μm单元的精细网格。用拉氏程序计算相同的问题与CEL程序的计算结果进行比对。如图3，若不进行重分重映，气体激波第一次汇聚时，拉氏气区网格扭曲。这说明二维拉氏程序计算均匀压缩问题时，很难得到精细的气区流场结构。为了进一步比较各飞层的界面走时，改用一维拉氏程序重新计算。计算结果如图4。由图可知，两种程序的飞层界面几乎重合，最大误差小于1%。以上结果说明CEL程序能够在保障飞层精度的前提下，得到高精度气区流场结构。

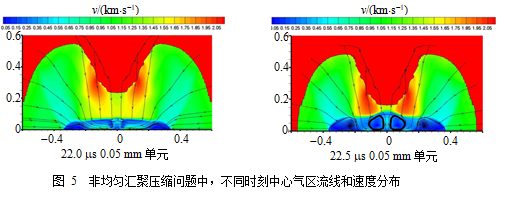
模拟非均匀压缩问题(相关参数引自张崇玉等开展的非均匀柱面压缩实验)时，气区采用50万个50 mm单元的精细网格，得到的气区结构如图5。22 ms在气区流场激波反射后出现了两个极小的漩涡结构。0.5 ms后，两个漩涡进一步扩大加强，流场中心还出现两个新的漩涡。四个漩涡会促进中心气区流场混合过程的发展，对于研究压缩过程产生的微喷、流体力学不稳定性以及介质混合等问题具有一定的参考价值。另外在飞层边界还可以观察到十分严重的网格扭曲，甚至自相交。这说明CEL方法具有较强的抗大变形能力，即使拉氏边界网格严重扭曲，也能持续计算并得到相对精确的气区流场。